In contrast to a normal GROMACS workflow, in this example we will not invoke pdb2gmx to build the topology. It will be constructed completely by hand using a simple text editor. The force field chosen for this exercise is OPLS-AA. The topology can be downloaded here. In this step, we will examine its contents to explain the logic behind its construction. The corresponding coordinate file for a single CO₂ molecule can be downloaded here.

First, we consider the distribution of mass in the molecule. Two mass centers are used to desribe the complete mass of the CO₂ molecule. From the topology, it can be seen how the total mass of the molecule was calculated in order to be redistributed between the two mass centers.

; Moment of inertia and total mass must be correct
; Mass is easy - virtual sites are 1/2 * mass(CO2)
;
; Total mass = (2 * 15.9994) + 12.011 = 44.0098 amu
;    each M particle has a mass of 22.0049 amu

The calculation for the moment of inertia is more difficult, but can be calculated from basic equations. The moment of inertia for a linear molecule consisting of three atoms (essentially a triatomic linear rotor) is: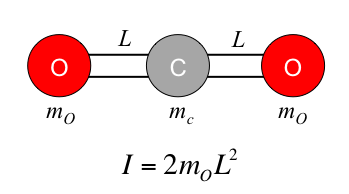

The moment of inertia for a diatomic molecule is: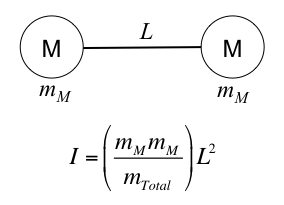

The value that is most straightforward to calculate first is the moment of inertia for CO₂, since we know all the quantities involved. The mass of an oxygen atom in OPLS-AA is 15.9994 amu and the C=O bond length is 0.125 nm. Substituting these values into the triatomic linear rotor moment of inertia equation above (and ignoring SI units because we will just have to convert back later), we obtain a value of 0.500 amu nm². We can then solve the diatomic molecule moment of inertia equation to obtain the separation of the two mass centers. Using a mass of 22.0049 amu for each mass center, we obtain a separation of 0.213173 nm for the distance between the mass centers. We set this value as a constraint in the topology. We use a constraint rather than a normal harmonic bond because (1) this value should remain invariant and (2) we eliminate the need to define new bonded parameters in the force field.

Now that we know the separation of the mass centers that reproduces the moment of inertia of our CO₂ molecule, we need to define the mechanism by which the virtual C and O sites are to be constructed. Virtual sites can be constructed in a linear fashion (using type 2 virtual site geometry and defined in a [ virtual_sites2 ] directive) as a fraction of the distance between two mass centers. In the topology, a value of a is given, corresponding to this fraction. The virtual site is then placed at a distance of a x b_ij from the first of the two given reference atoms, where b_ij is the bond length between the two atoms.

We begin with the easiest virtual site to place. The carbon atom is placed in the center of the molecule, exactly in the middle of the two mass centers. Thus in the topology, we define this site as occurring at a value of a = 0.5 and hence in the topology we define:

     2   4   5      1   0.5000      ; right in the middle

Constructing the positions of the oxygen virtual sites is more difficult. These virtual sites do not occur between the two mass centers, rather they are beyond the distance between atoms M1 and M2. Thus, the value of a must be larger than 1, such that the virtual site position is outside the M1--M2 length. Since the value of a is given as a fraction of the total length between the relevant mass centers, we need to calculate its value. This calculation is given in the topology. Briefly:

1. The C=O bond length is 0.125 nm
2. The M1--M2 constraint length is 0.213173 nm, therefore half this distance is 0.1065865 nm
3. Therefore, the O virtual site extends 0.0184135 nm beyond the M1--M2 distance
4. Thus, the value of a is (0.213173+0.0184135)/0.213173 = 1.0851116

In the topology, there are two lines for these O virtual sites, relative to each mass center, M1 (atom 4) and M2 (atom 5):

     1   4   5      1   1.0851116   ; relative to mass center 4, extends beyond mass center 5
     3   5   4      1   1.0851116   ; as in the case of site 1